[10000ダウンロード済み√] 三角比 辺の長さ 求め方 182104-三角比 辺の長さ 求め方 正弦定理

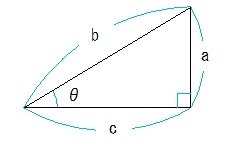
直角三角形の各辺の長と三角比の関係 直角三角形の1辺の長さと，直角でない1つの内角がわかっている場合の各辺の長さを三角比を用いて表す． AB = c とすると， sin θ = BC AB より， BC = c sin θ cos θ = AC AB より， AC = c cos θ BC = a とすると， sin θ = BC AB より}{ 11\sqrt{ 2 } }\)になります。 この辺の比を覚えておくことで、底辺から斜辺の長さを求めたり、またその逆のことができます。 数学三平方の定理が成り立つ三辺の比：最重要7パターン ～受験の秒殺テク（5）～ 絶対におぼえておきたい直角三角形TOP7 高校受験を控える中学3年生の皆さんに、わずかな時間で正解を出すことができる"秒殺テクニック"を紹介していきます。

外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ

三角比 辺の長さ 求め方 正弦定理

三角比 辺の長さ 求め方 正弦定理- 押さえておきたい三辺の長さの比 今回は 三平方の定理 も踏まえつつ、二等辺三角の性質と辺の長さの求め方についてご紹介します。 抑えておくべきポイントは三角形毎の辺の比率です。 目次 非表示 1 直角二等辺三角形の性質と辺の比率 11 性質 12 辺の比率 2 直角二等辺三角形の辺の長さの求め方 3 正三角形の性質と辺の長さやっぱり、敷地の面積を求めていたのか！ただ、三角形の辺の長さを測るだけで面積が求められるの？ 「ヘロンの公式を使えばいいんです」。 ヘロンの公式が使われていた 図3 三角形から生まれる美しい数のリズム「三角比」。

三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ

2辺a,bと高さ（角Cは鋭角）選択で 辺a=5 辺b=6 高さ=3で計算したとき、角Aの値がマイナスになります。 keisanより ご指摘ありがとうございます。修正いたしました。直角三角形の左端の角度が30度の時のそれぞれの辺の長さの比を覚えていますか？ 三角形の比についてよくわからない方は、三角比（30°,45°,60°） をみてください。 それでは、sin30°、cos30°、tan30°の求め方を説明していきます。 sin30°の求め方 上の直角 sinθ＝ 対辺 ／ 3 より 対辺 ＝ 3 sinθ となります。 このとき、 対辺の長さが座標軸における点Pのy座標 となります。 cosθ＝ 底辺 ／ 3 より 底辺

− 95 − 高校講座・学習メモ ベーシック数学 29 三角定規の性質 問題3 1辺の長さが1の正八角形の面積を求めなさい。 考え方 右図のように，1三角比は，直角三角形の辺の比を表します。 長さがわからない辺があるので，まずは三平方の定理を利用してすべての辺の長さを求めましょう。 次に，定義に従って三角比の値をそれぞれ求めます。 今回の問題では が左下にあるので簡単に求められます。 直角三角形の底辺と高さから傾斜角と斜辺を計算します。 底辺と高さから角度と斜辺を計算 高精度計算サイト ゲストさん

三平方の定理 特別な直角三角形の3辺の比｜ Excel三角形の斜辺の長さ・高さ・底辺の長さを残りの2辺からする方法直角三角形の辺の求め方 関連ページ Excelデータ分析ツール使用の前準備 度数分布表とヒストグラム Excel平均とは？三角比の定義 三角比の仕事は，直角三角形の辺を角度を使って対応づけることです． まず，直角三角形の直角でない角度の1つを としておきます （普通は角度の変数に （シータ）が使われますが，別に記号は何でもいいので にしときます）． このとき三角形の各辺がどういう名前で呼ばれるどのように大きな三角形の辺の長さも，すぐに求めることができる。 直角三角形の場合，直角以外の1 つの角が決まると相似となるので， 右図の角 または が決まれば辺の比が決まる。

簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく

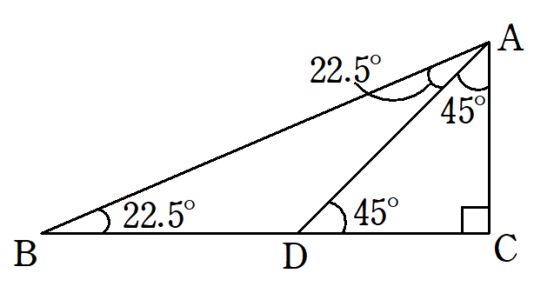
22 5 の三角比 Fukusukeの数学めも

 まず覚えておいておくべき直角三角形の辺の比は、 12√3 だよ。 この辺の比になる直角三角形の角度は、 30° 60° 90° になってるんだ。 例えば、次の直角三角形ABCがあったとして、辺BCの長さが2cmだったとしよう。正弦定理から，三角形の辺の長さを求める計算について ABCにおいて a = 3 ， A = 60°， B = 45°のとき b を求めよ。 という問題がありますが， これを定理にあてはめていって， b = 3 / sin60°× sin45° まではつくれるんですが，そこから (3 ÷ √3/2 ) × 1/√2= 6/√6=√6 というのになるのが，意味がわかりません。 なぜルートが出てくるのですか？ (3 ÷√3/2)×1/√2が，もう何 三平方の定理を使って直角三角形の辺の長さを計算したい！ どうも、Drリードだぞい。 中3数学では、 三平方の定理（ピタゴラスの定理） を勉強してきたよな？ 簡単に復習すると、 直角三角形の直角をはさむ2辺の長さをa、b、斜辺の長さをcとすると、 a²＋ b² = c² が成り立つ ってやつだったな。 さあ、この定理を使いこなせるようになるんだぞ。

高校数学の三角比について質問です 図において Cdとbcの辺の長さ Yahoo 知恵袋

余弦定理で角度を求める方法 数学の星

三角形とは？面積の公式や、角度・辺の長さ・重心の求め方 Excel三平方の定理で直角三角形の辺の長さ、面積、角度を 高校数学Ⅰ 三角比辺の長さの求め方まとめと問題 manab三角形の辺の長さを求めるときの三角比の値 下の図の x の値を求めよ。 これを解こうとすると，sin45°，sin60°という三角比が出てきました。計算すると、 4 9 = c × c 13 = c × c よって、長い辺の長さは c = 13 （二乗して 13 になる正の数）となります。 では、 13 はどれくらいの長さでしょうか？ 3 × 3 = 9 c × c = 13 4 × 4 = 16 なので、 13 は 3 より大きくて 4 より小さい数だと分かります。

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信

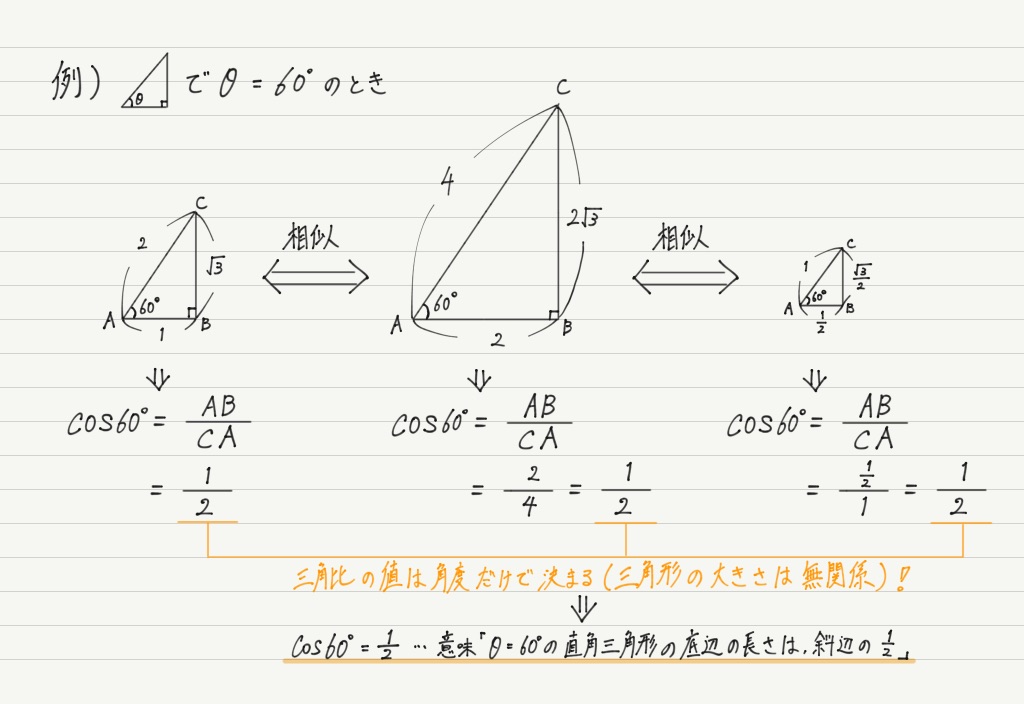
三角比と三角関数 高校物理をあきらめる前に 高校物理をあきらめる前に

 定義や辺の長さの比、面積の求め方 受験辞典 直角二等辺三角形とは？ 定義や辺の長さの比、面積の求め方 この記事では、「直角二等辺三角形」の定義や公式、辺の長さの比などについて解説していきます。 また証明問題もわかりやすく説明していく三角比1（tanθ） 三角比2（sinθ,cosθ） 超重要 30°と60°の三角比;三角形の「2辺の長さの比」が正弦の値になるのは直角三角形の場合だけで、それ以外の場合には sin A の値は「2辺の長さの比」にはなりません。 （右図イのような場合も含めて）一般に、 角度 A の値によって sin A の値が決まり、これとは別に辺の長さが決められている と考えることが重要です。

3

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 ガジェット通信 Getnews

5年 算数 学研教育情報資料センター 学習相談 小／算数／5年／数量関係／ 文字と式／理解シート 三角形の面積から，辺のまた，用いる三角形によって半径の取り方は，適当に決めればよいのです。なぜなら，左の図を見てみれば分かるように，三角形によって 3 辺の長さは異なりますが，3 辺の比は一定です。< 三角比と辺の長さ> 問1 三角関数表を用いて次の問に答えよ。 (1)図1のab，bcの長さを求めよ。 (2)図2のdh，ehの長さを求めよ。 問2 図3 の三角形abc において， abとbcをr とθで表せ。 問3 図4においてehとdhの 長さをr とθで表せ。 (ただしθは鈍角である。

直角三角形の辺を求める Youtube

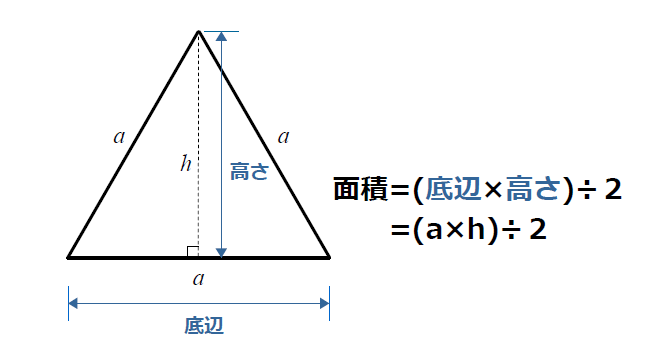
正三角形の面積計算 ゆるゆるプログラミング

となることがわかります。 次に円の中心 O から辺 BCに向かって垂線を下ろし、辺 BC との交点を点 F とします。 また OB=OC= R より、 BOC は二等辺三角形だとわかりますね。 よって \\ \begin {eqnarray} \angle BOF &=& \angle COF \\ &=& \frac {1} {2}\angle BOC \\ &=& \frac {1} {2}\times2\angle BAC \\ &=& \angle BAC ・・・ (1) \end {eqnarray} \\「三角比」で長さを求める！ 今回は、 「三角比を利用した長さの求め方」 を学習しよう。 実は、直角三角形の 「斜辺」 と、 「角度θ」 が分かっていれば、三角比を利用して 「高さ」 と 「底辺」 を求めることができるんだ。ときは、三辺の比が（解説3）のように求められる。 しかし、それ以外の角、たとえば、右図のような直角三角形においては 三辺の比は分からない。 b このような場合には、教科書，傍用問題集の末尾にある 「三角比の表」を用いて求めるとよい。

三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典

三角比の定義は １分でわかる定義 覚え方 表 直角三角形と単位円との関係

高校数 三角比 三角形の垂線の長さ オンライン無料塾 ターンナップ Youtube

Q Tbn And9gcq7h6dlzvq5e0plulfvxu64dpvadasyky0sizoi2drjv Uyz1m5 Usqp Cau

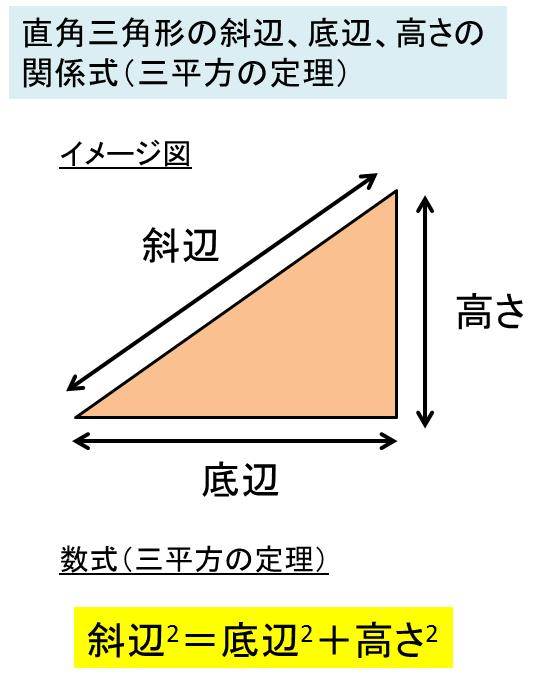
Excel 三角形の斜辺の長さ 高さ 底辺の長さを残りの2辺からする方法 直角三角形の辺の求め方

三角比と年周視差 星のこと

三角比で辺の長さを表す問題がいまいちよく分かりません 求め方のポイントなど Yahoo 知恵袋

高校数学 三角比を利用した長さの求め方2 例題編 映像授業のtry It トライイット

二辺挟角から残りの辺を求める Schoolmath S Diary

数i 基本的な三角比の値

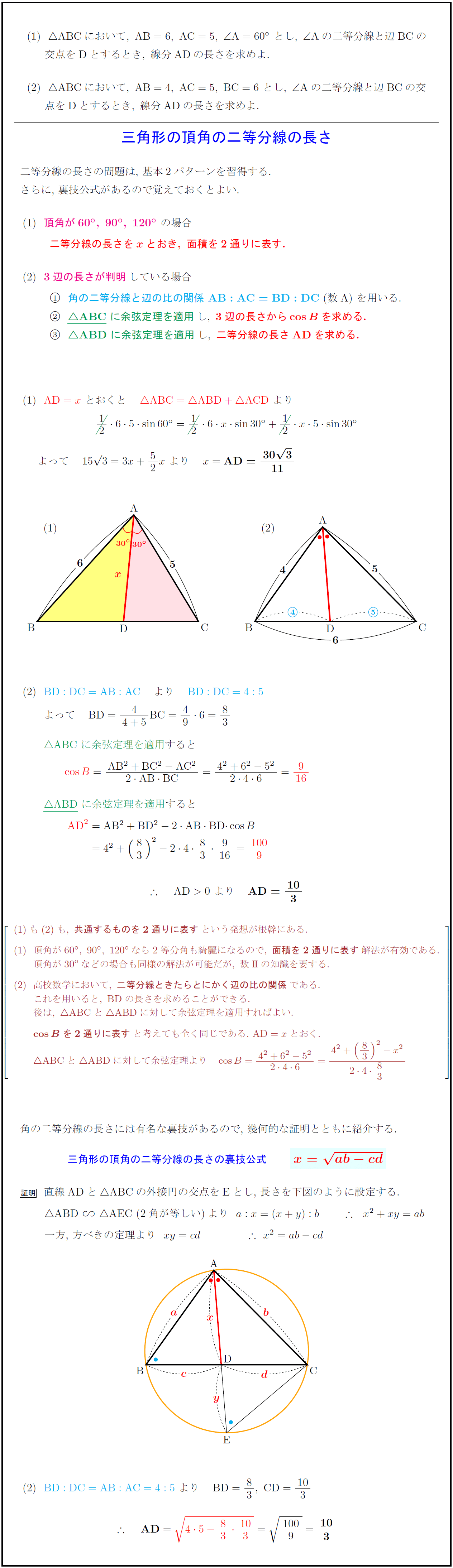
高校数学 三角形の頂角の二等分線の長さ 基本2パターン 裏技公式 X Ab Cd とその証明 受験の月

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ

底辺と角度から 高さを求める ある高さの木から 10m離れて 木の 数学 教えて Goo

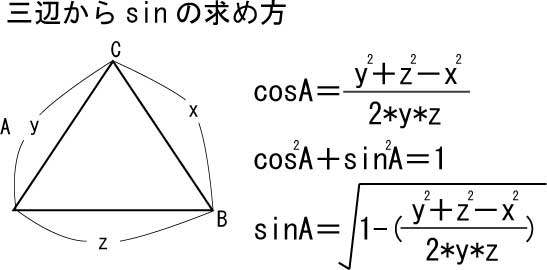
正弦定理 余弦定理の求め方 三角形いろいろ 三角比の応用 エミュー

直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典

日曜大工で使う数式

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信

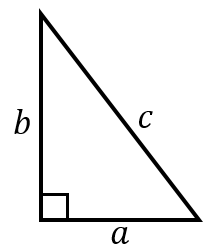
直角三角形の辺の長さの求め方と計算ツール 具体例で学ぶ数学

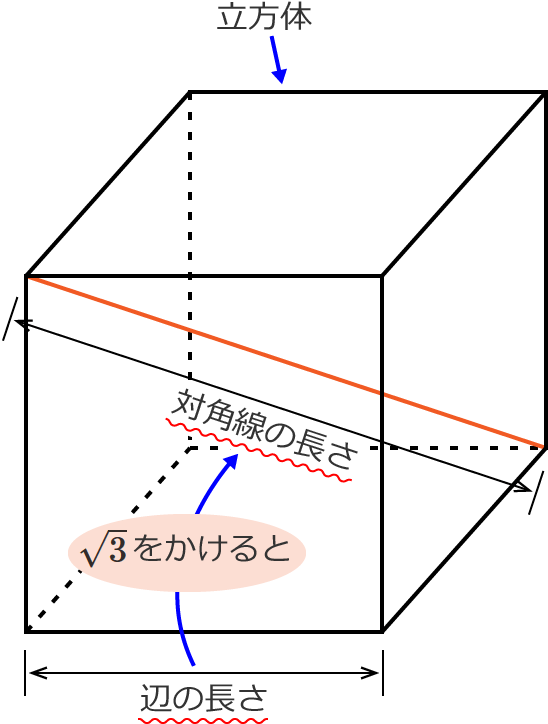
立方体の対角線の長さの求め方

Excel 三角形の角度を底辺や斜辺 高さから求める方法 直角三角形の角度の計算

ヘロンの公式で三角形の面積を求める 三辺の長さがわかっているときはコレ 数学の面白いこと 役に立つことをまとめたサイト

高校数学 ３辺 三角形の面積 を求める方法 映像授業のtry It トライイット

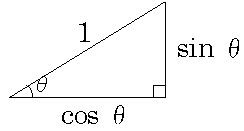
三角関数の初歩

外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ

三角比の表の求め方について質問です 求め方を調べるとこんな感じに三 Yahoo 知恵袋

30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学

高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月

簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

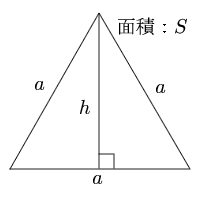
正三角形 高さから辺と面積 三角形の計算 計算サイト

三角形面積求め方 三角形とは 面積公式 角度 辺の長さ 重心 比の計 Jbqhd

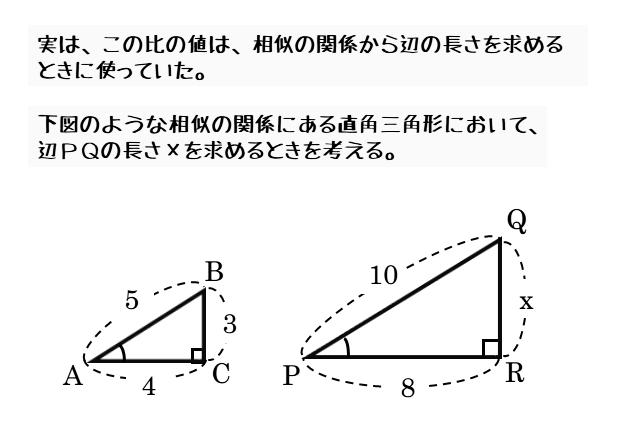
図形と計量 三角比の定義について 日々是鍛錬 ひびこれたんれん

高校数学 三角比を利用した長さの求め方1 練習編 映像授業のtry It トライイット

数i 基本的な三角比の値

高校数学 三角比を利用した長さの求め方2 例題編 映像授業のtry It トライイット

底辺と高さから角度と斜辺を計算 高精度計算サイト

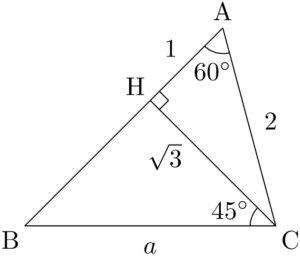
数学ia 三角比の応用 大学入試数学の考え方と解法

わかりやすい三角比と基本公式 Irohabook

高校数学 3辺の長さが等しい 三脚型 四面体の体積 受験の月

高校数学 三角比 余弦定理の公式を証明 図を使って丁寧に説明 数学の面白いこと 役に立つことをまとめたサイト

直角 三角形 辺 の 長 さ 求め 方 直角三角形の解法 1 Documents Openideo Com

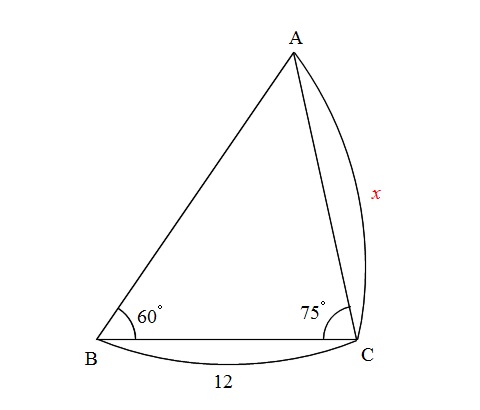
三角形で角度が2つ分かっているのに正弦定理も余弦定理も使えない

中3数学 3 4 5の直角三角形の辺の長さを求める3つの問題 Qikeru 学びを楽しくわかりやすく

15 75 105 165 の三角比 数学i フリー教材開発コミュニティ Ftext

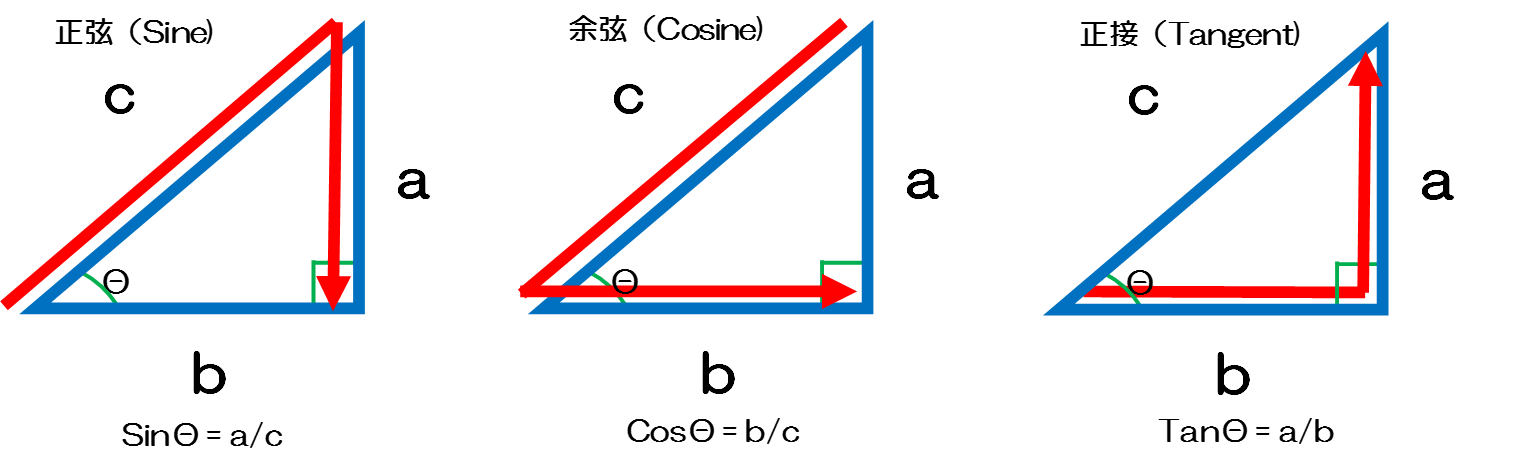
Vba 三角比をもとめる Sin関数 Cos関数 Tan関数 角度をもとめる Atn関数

円周率を考えると三角比が何なのかよく分かる Sharewis Press シェアウィズ プレス

三角比の測量への利用 数学解説ブログ つくば市の 数学 算数 物理に強い プロ家庭教師 長通幸大 発信

正弦定理から 三角形の辺の長さを求める計算について 数学 苦手解決q A 進研ゼミ高校講座

直角三角形の辺の長さ 合同条件 面積について アタリマエ

タンジェントとは何か 中学生でも分かる三角関数の基礎

高校数学 三角形の辺と角の関係 映像授業のtry It トライイット

交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー

Math 90 30 60 の直角三角形 辺の長さで成り立つこと 働きアリ

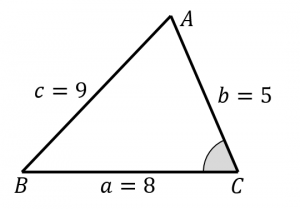
三角形の面積を３辺の長さから求める２つの方法 具体例で学ぶ数学

三角比と辺の長さの関係は 1分でわかる求め方 角度と辺の長さの比

三角形の辺や角が与えられたとき残りの辺や角を求める方法 数学の偏差値を上げて合格を目指す

1

三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube

高校数 三角比 三角形の面積 鈍角三角形 オンライン無料塾 ターンナップ Youtube

三角関数 1 Cg 数学 07ad

鈍角の三角比

三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ

黄金三角形による18 シリーズの三角比 おいしい数学

高校数学 三角比 三角比の求め方と覚え方 Sin Cos Tan 数学の面白いこと 役に立つことをまとめたサイト

ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

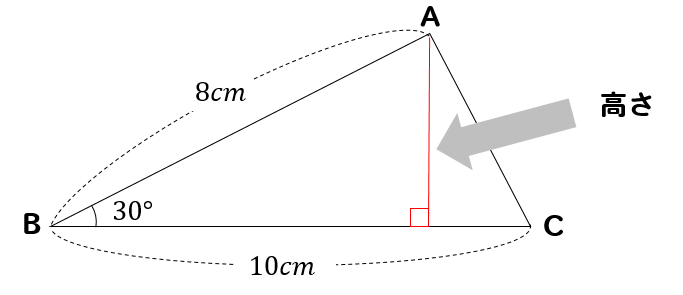
小学算数 30度の三角形ってどうやって面積求める 辺の比は 数スタ

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信

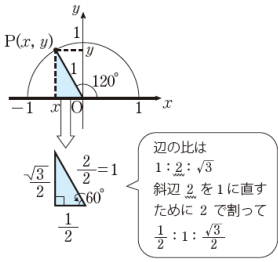
90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座

三角比を考え方から理解する 有名角の三角比も説明

1

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

数学の勉強 三角比

中3数学 3 4 5の直角三角形の辺の長さを求める3つの問題 Qikeru 学びを楽しくわかりやすく

直角三角形ではない場合ピタゴラスの定理はどう使えるのでしょうか Quora

三角形の３辺から角度を計算 高精度計算サイト

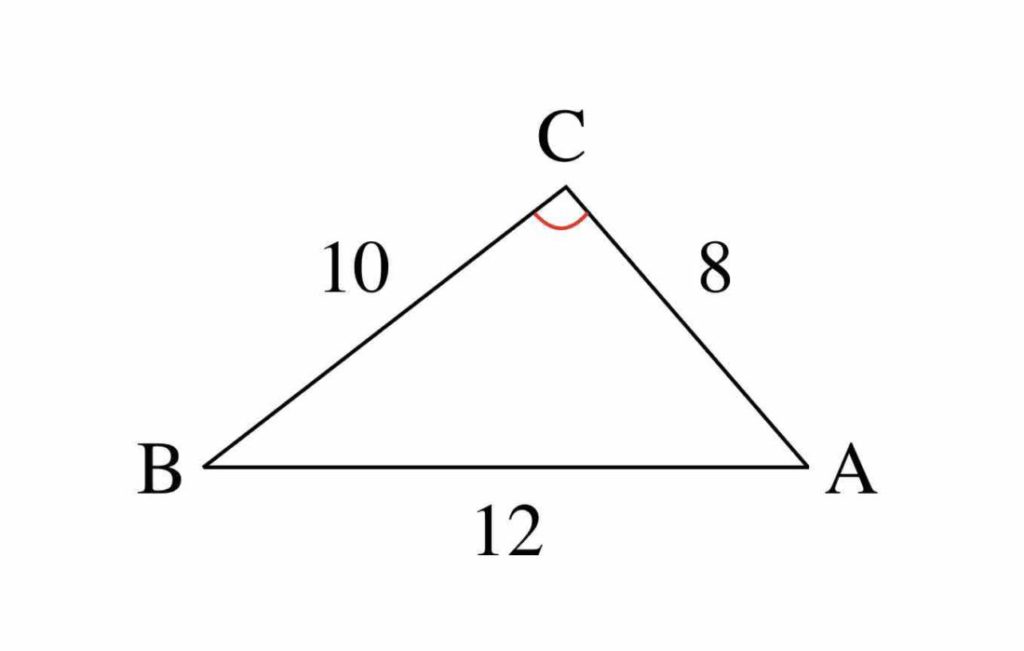
三角比を用いた面積計算をマスターしよう スタディクラブ情報局

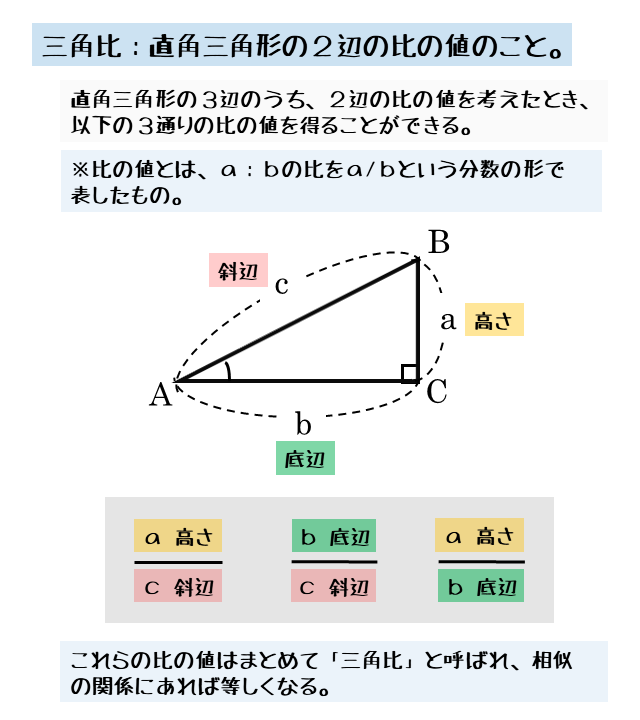
図形と計量 三角比の定義について 日々是鍛錬 ひびこれたんれん

反射で求める三角比と辺の長さ 高校生 数学のノート Clear

高校数学 三角比 辺の長さの求め方まとめと問題

三角関数 ｎｃプログラム基礎知識

三角関数は何に使えるのか サイン コサイン タンジェントの活躍 Qiita

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ

三角定規の直角三角形のときは 比の計算で簡単に求めよう 中学や高校の数学の計算問題

三角比から辺の長さを求める 数学i フリー教材開発コミュニティ Ftext

高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト

余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ

三角関数について

数i 基本的な三角比の値

三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ

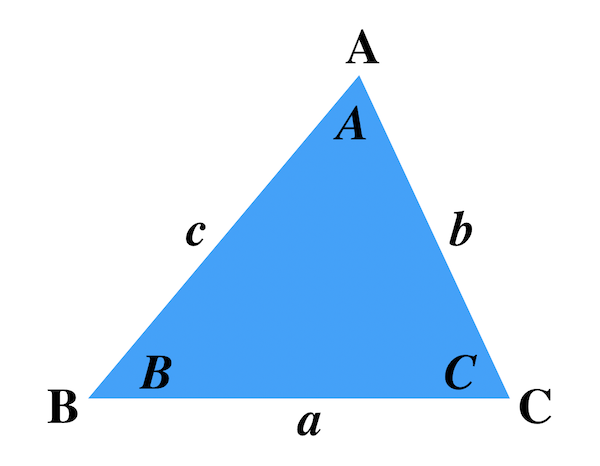
三角比 正弦定理と余弦定理を詳しく解説 スタディクラブ情報局

三角比を使って円に内接する四角形の辺の長さ 面積を求める方法 数学i By Okボーイ マナペディア

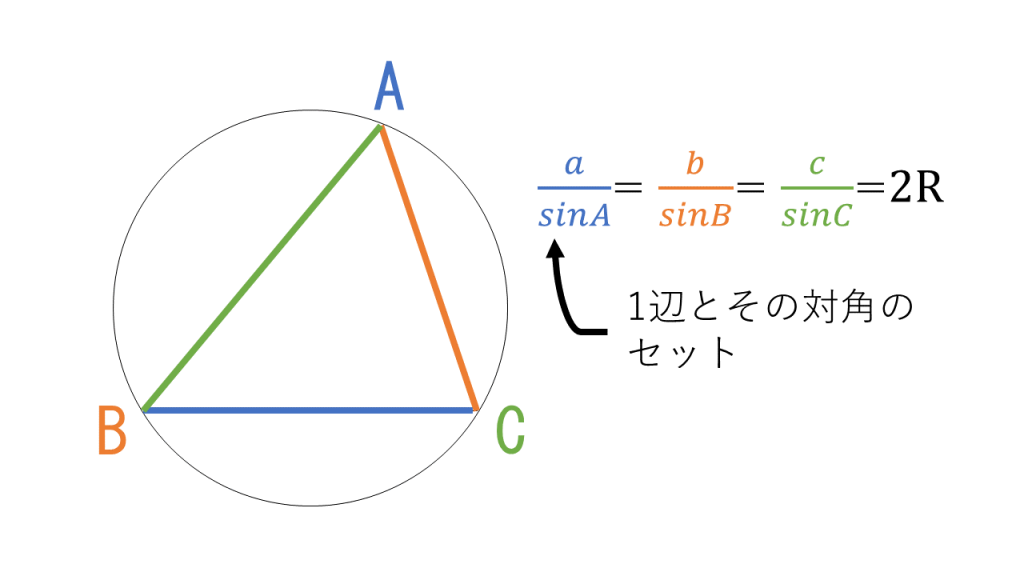
3分で分かる 三角形の外接円の半径の長さの求め方をわかりやすく 合格サプリ

三角比について

Incoming Term: 三角比 辺の長さ 求め方, 三角比 辺の長さ 求め方 正弦定理,